1.1 Propiedades y tipos de triángulos
El triángulo es una figura geométrica de tres lados y tres ángulos.
Sus principales propiedades son:
-La suma de sus ángulos es de 180º.
-La suma de dos de los lados siempre es mayor que el lado sobrante.
-El valor de un ángulo exterior es igual al de los adyacentes interiores.
-Si el triángulo tiene dos lados iguales, los ángulos opuestos serán iguales.
Según sus lados:
Triángulo equilátero (3 lados iguales)
Triángulo isósceles 2 lados iguales
Triángulo escaleno 3 lados desiguales
Según sus ángulos:
1.2 Rectas y puntos notables en el triángulo
Incentro
El incentro es el centro de la circunferencia inscrita al triángulo, por lo que la distancia a cada uno de sus lados es la misma.
Baricentro
El baricentro (también llamado centroide) de un triángulo es el punto de intersección de las medianas de dicho triángulo.
Circuncentro
El circuncentro de un triángulo es el centro de la circunferencia circunscrita al triángulo, por lo que la distancia a cada uno de sus vértices es la misma.
Ortocentro
El ortocentro de un triángulo es el punto de intersección de las tres alturas del triángulo.
1.3 El teorema de Pitágoras
El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las respectivas longitudes de los catetos.
1.3.1 Demostración gráfica
1.4 El teorema de Tales (vídeo: Les Luthiers - Teorema De Thales
triángulos semejantes. ¿Cómo calcular
la altura de un árbol a partir de su sombra?
El objeto es vertical y su sombra horizontal. La inclinación de la luz del sol será la que determine la longitud de la sombra. Con el punto más alto del objeto, el punto donde éste llega al piso y el punto más lejano de la sombra, armamos un triángulo imaginario.
Nominamos los vértices con las letras A, B y C.
Tenemos que averiguar cuanto mide el lado AB, que por ahora será igual a X.
Medimos la longitud de la sombra, que es el lado BC. Supongamos que tiene 21.36 metros.
Con ese dato todavía no podemos calcular X.
El paso siguiente es tomar un referente de un metro de altura (A’B’) y medir su sombra (B’C’). Supongamos ahora que la sombra de éste objeto es igual a 1.78 metros. Esto se tiene que hacer enseguida de medir la primera sombra, para que no haya una variación en el ángulo de la luz solar.
Nominamos los vértices con las letras A, B y C.
Tenemos que averiguar cuanto mide el lado AB, que por ahora será igual a X.
Medimos la longitud de la sombra, que es el lado BC. Supongamos que tiene 21.36 metros.
Con ese dato todavía no podemos calcular X.
El paso siguiente es tomar un referente de un metro de altura (A’B’) y medir su sombra (B’C’). Supongamos ahora que la sombra de éste objeto es igual a 1.78 metros. Esto se tiene que hacer enseguida de medir la primera sombra, para que no haya una variación en el ángulo de la luz solar.
2. Lugares geométricos
Un lugar geométrico es un grupo de puntos que cumplen una misma propiedad, escrita en lenguaje algebraico.
2.1 La mediatriz y la bisectriz
Un lugar geométrico es un grupo de puntos que cumplen una misma propiedad, escrita en lenguaje algebraico.
2.1 La mediatriz y la bisectriz
La mediatriz de un segmento es la recta perpendicular al segmento, que pasa por su punto medio, dividiendo al segmento en dos partes iguales.
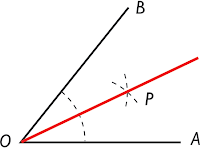
La bisectriz de un ángulo es la semirrecta, que tiene su origen en el vértice del ángulo y que lo divide en dos ángulos iguales.
2.2 Cónicas
2.2.1 ¿Qué es una cónica?
La cónica es la curva obtenida al cortar la superficie cónica por un plano. Existen varios tipos:
2.2.2 Circunferencia
Es la sección formada al ser cortada por un plano perpendicular al eje.
2.2.3 Elipse
Es la sección formada al ser cortada por un palo oblicuo al eje, pero no paralelo a la mediatriz.
-Método del jardinero para la obtención de una elipse
Se clavan dos estacas en el suelo. Después, se coge una cuerda de longitud mayor a la distancia entre las dos estacas. Más tarde, se coge un ´lápiz/bolígrafo y se coloca entre la cuerda. Por último, se recorre con el lápiz hasta formar la figura.
-Mesa de billar elíptica
Es una mesa de billar con forma de elipse. La peculiaridad de esta mesa no radica en su forma, sino que es especial, además, porque la bola siempre entra en el agujero (foco).
2.2.4 Hipérbola
Es la sección formada al ser cortada por un palo oblicuo al eje, formando un ángulo menor al que forman la generatriz y el eje y.
-Lámpara hiperbólica
Son lámparas, muy usadas en habitaciones de casas, que forman figuras con forma de hipérbole con la luz.
2.2.5 Parábola
Es la sección producida por un plano oblicuo al eje, siendo paralelo a la generatriz.
-Antenas parabólicas y horno solar
Son aparatos usados para enviar señales de radio o TV. La razón por la que tengan forma de parábola es porque los rayos paralelos al eje de simetría de la parábola son reflejados por la misma hacia su foco.
-Espejo parabólico
Son espejos que tienen son usados para aparcamientos, ya que permiten un mayor ángulo de visión, perfecto para evitar accidentes.
3.2 Ejercicios de vectores y traslación
3.2.1 Dados los vectores u=(4,3) y v=(-1,4), hallar:
a) su representación gráfica en un sistema de coordenadas
b) los vectores u + v y u - v por la regla del paralelogramo
c) las componentes de los vectores anteriores
d) el módulo de cada uno de los vectores
Los componentes del vector u+v son (3,7), de u-v (5,-1), de u(4,3) y de v(-1,4)
los módulos del vector u+v es 7,61, de u-v es 5,09
3.2.2 Dibuja las figuras trasladadas de las siguientes en una traslación de vector guía u(4,3):
3.3 Giros
3.3.1 Ejercicio: Escribe la inicial de tu nombre y haz varios giros con ella.
3.4 Simetría.
Ejercicios 3.4.1
Dado el triángulo de vértices A(-2,2), B(6,-1) y C(7,5) se pide:
Ejercicios 3.4.1
Dado el triángulo de vértices A(-2,2), B(6,-1) y C(7,5) se pide:
a) dibujar el triángulo
b) hallar el triángulo simétrico respecto del centro de simetría O(0,0)
c) hallar el triángulo simétrico respecto del eje OX
3.4.3 Carlos y Fernando están jugando al billar. En un determinado momento las bolas se encuentran en las posiciones indicadas por el dibujo. Indica el camino que debe seguir la bola A para querebotando en la banda MQ golpee a la bola B .
Indica el camino que debe seguir la bola A para que rebotando en la banda NP y PQ golpee a la bola B.
3.4.4 Inventa un abecedario simétrico y escribe una frase.
3.5 Frisos, mosaicos y cenefas
Friso : es el cubrimiento de la región del espacio de longitud infinita pero de anchura finita, limitada por dos rectas paralela.
Mosaicos : Los mosaicos, al igual que los frisos, se pueden generar a partir de un motivo mínimo mediante la combinación de diferentes movimientos.
Cenefas Es un elemento decorativo largo y estrecho que se coloca en una pared rodeando su perímetro o como marco de otros elementos decorativos.
3.6 MC. Escher
Maurits Cornelis Escher (1898-1972) es uno de los artistas gráficos más famosos del mundo. Su arte es disfrutado por millones de personas en todo el mundo, como se puede ver en los muchos sitios web en Internet.
Él es el más famoso por sus supuestos construcciones imposibles , como ascendente y descendente , la relatividad , sus impresiones de transformación , como la metamorfosis que ,Metamorfosis II y Metamorfosis III , Cielo y Agua I o reptiles .
Pero también hizo algo de trabajo maravilloso, más realista durante el tiempo que vivió y viajó por Italia.
Castrovalva por ejemplo, donde ya se puede ver la fascinación de Escher para alta y baja, cerca y lejos.La litografía Atrani , una pequeña ciudad en la costa de Amalfi se hizo en 1931, pero regresa por ejemplo, en su obra maestra La metamorfosis I y II .
MC Escher, durante su vida, hace 448 litografías, xilografías y grabados en madera y más de 2000 dibujos y bocetos. Al igual que algunos de sus famosos predecesores, - Miguel Ángel, Leonardo da Vinci, Durero y Holbein-, MC Escher era zurdo.
Aparte de ser un artista gráfico, MC Escher ilustra libros, tapices diseñados, los sellos y murales. Él nació en Leeuwarden, Holanda, como el cuarto y último hijo de un ingeniero civil. Después de 5 años, la familia se trasladó a Arnhem, donde Escher pasó la mayor parte de su juventud. Después de fallar sus exámenes de secundaria, Maurits en última instancia, se inscribió en la Escuela de Arquitectura y Artes Decorativas de Haarlem.
4. Resumen de áreas y volúmenes de figuras conocidas
5. La esfera y el globo terráqueo
5.1 Elementos principales de la esfera.
●Centro: Punto interior que equidista de cualquier punto de la esfera.
●Radio: Distancia del centro a un punto de la esfera.
●Cuerda: Segmento que une dos puntos de la superficie.
●Diámetro: Cuerda que pasa por el centro.
●Polos: Son los puntos del eje de giro que quedan sobre la superficie esférica.
5.2 Elementos de la esfera terrestre.
- Meridiano de Greenwich: También conocido como meridiano cero, meridiano base o primer meridiano, es el meridiano a partir del cual se miden las longitudes. Se corresponde con la circunferencia imaginaria que une los polos y recibe su nombre por pasa por la localidad inglesa de Greenwich, en concreto por su antiguo observatorio astronómico.
- Ecuador: Es el plano perpendicular al eje de rotación de un planeta y que pasa por su centro. Divide la superficie del planeta en dos partes: el hemisferio norte y el hemisferio sur. Por definición, la latitud del ecuador es 0°
- Paralelos: Circunferencias obtenidas al cortar la superficie esférica con planos perpendiculares al eje de revolución.
5.3 Los husos horarios, la hora local solar y oficial.
Los husos horarios son cada uno de los 24 sectores esféricos en que se divide la superficie de la Tierra. Resultan de repartir los 360º de la esfera terrestre entre las 24 horas que invierte en dar una vuelta completa sobre su propio eje.
Cada huso horario mide 15 grados (360º / 24 horas = 15º). 15º = 1 hora.
Para conocer la hora en algún lugar del mundo se toma como referencia el meridiano 0 ( Greenwich ). A partir de él se añade una hora por cada huso horario que se recorra hacia el este y se resta una hora por cada huso que se recorra hacia el oeste.
5.4 El método de Eratóstenes para calcular el diámetro de la circunferencia terrestre
